Implementing a Fuzzy Search engine using Local Sensitive Hashing

What:

Fuzzy Search or approximate string matching involves, as the name suggests finding best possible candidates in an already stored collection of strings given some pattern string.

Given some query-string(pattern), we would like to return a set of suggestions from the above said collection, even though there may not be an exact match. Such functionality leads to robust text interfaces, as this would tolerate some error in the input text to return desired results with high probability.

Actual such implementation would depend upon the edit-measure and actual algorithm used to calculate that edit-measure for all possible candidates. Generally Levenshtein_distance is used as an edit-measure which works by calculating the number of primitive operations needed to be done to transform a pattern string into one of possible candidates. (hence resulting algorithms' runtime are proportional to length of pattern string.) Most of the fuzzy-search implementations are based on levenshtein-distance as en edit-measure.

More edit-measure include techniques like Locality Sensitive Hashing, which we would try to use for our implementation. It involves generating a Hash. Lsh generates hashes to maximize collisions unlike traditional hashes like MD5 and SHAxx hashes. (where a single byte difference results in a totally different hash). Generated Hashes can be directly compared to have a measure of similarity between two strings or a sequence of bytes.

If it would work, then during querying stage, resulting algorithm would depend only upon the size of COLLECTION (N), as comparing two hashes would take same amount of time, irrespective of original string from which hash was produced.

This also lends itself to a map-reduce pattern (if needed), i.e allowing whole collection to be processed concurrently as each of value in N is supposed to be independent.

LSH is a concept and actual implementation of such concept would involve choosing a HASH function, which vary according to the application we would be writing implementation for. For our use case we use Pearson Hashing, which is a very fast and simple hashing algorithm designed for fast execution on processors with 8-bit registers. It works with sequence of any length and outputs a single byte ([0-255]) that is strongly dependent on every byte of the input. We control the number of bytes this would take as input (window-size).

Using a hash function LSH implementation hashes similar input items into the same buckets with high probability. Numbe of buckets is another parameter we decide upon in a particular implementation.

This implementation use a BUCKET SIZE of 64, where each bucket is represented using 2 bits. Hence final hash is atleast 128 bits long, which translates to a hexadecimal string of length 32.

Since number of buckets is much less than possible data combinations, it can be viewed as another method for dimensionality reduction.

Using too many buckets may lead to empty buckets (hence no useful information ) , and too few buckets would lead to increase in false positives. For a good hash, 50% of buckets are supposed to be non-empty, if not resulting hash is supposed to be unusable. It would indicate not enough variation in the original data to generate a useful hash. We would be using it to extract possible candidates from a set of candidates, so actual score would not matter to us as much.

Final hash is generated by attending all the characters/bytes in the data in a sliding fashion. SLIDING WINDOW size is another parameter we chose for this LSH implementation. All the bytes inside a current WINDOW are passed through HASH function and collected in one of Buckets. Each buckets is divided into 4 levels which are encoded using 2 bits, (00, 01, 10, 11). Final hash is a collection of all such bits put together. Optionally a checksum can also be included in the final hash depending upon implementation.

Lsh implementations formally contains some other parameters like a threshold, approximation factor etc. In this case we are interested in sorting all candidates based on the score predicted on comparison. Actual value for that score wouldn't matter much, so we don't care much of other formal parameters. Any such implementation must predict a lower score for similar strings with very high probability and a relatively higher score for dis-similiar strings. Note that similarity is subjective here, and an exact definition of similarity would depend upon the application.

LSH in various forms is used in the computer security to identify binary file structures with known malware binary patterns, and also to identify the spam emails. Effectiveness would depend on the actual implementation, an implementation written for one application may not work as good for another domain.

The implementation i used is based on the Trendmicro's https://github.com/trendmicro/tlsh. Since there was no pure-python port i also ended up writing pure python implementation based on the corresponding JS port. To access more resources on LSH and ports for more languages checkout their repository.

Why (Motivation):

I work on Hachi, which is used to index semantic and meta-data for locally stored resources. As there could be lot of such meta-data, i wanted to allow for a robust search experience as user may not remember the exact information and which is what a fuzzy search is supposed to be good at. Also from beginning i tried to keep the dependencies for hachi to be minimal and isolated, in case i need to port code to system-level languages with a less mature packaging ecosystem.

Even though text-interfaces are used everywhere, a robust fuzzy search is not, in my opinion it should be dead easy to add fuzzy search to any existing interface be it CLI or Web-based. For existing implementations with no fuzzy-search, including a fuzzy search would only improve the interface if it doesn't have a signification run-time cost. API i envisioned was supposed to be like this:

stored_data = [];  # a collection of stored text strings, like possible commands for a CLI app, for which user want to provide suggestions for.

def append(new_data:str):
    # just append that to stored data
    # update necessary data-structure for fuzzy search, like calculating LSH hash and stuff
    pass

def suggest(query:str) -> list[str]:
    # just return the possible candidates sorted by probability/scores from stored_data, provided a given query.
    pass

def remove(data or index):
    # just remove this entry from stored_data, and corresponding fuzzy data-structures
    pass

Final implementation turned out to be dependency-free pure implementation in python, which can be included in existing implementations with no conditions.

How: (Code and logic):

LSH as discussed includes a Hash function which can be used to map a sequence of bytes to fixed size HASH, which then can be compared to other such hashes to get a measure of similarity. The actual underlying implementation expected at least 50 bytes to produce usable hashes, otherwise more than 50% of buckets would be empty and we wouldn't have a useful hash/measure for a given string/data.

This was a problem, since 50 bytes roughly translates to 50 characters (at least in ASCII). This may not be case for most of the data we would want to index. We would need to artificially increment the length of data being hashed in order to use this implementation. Any solution would include bias, as we would be augmenting the original data with some extra information. We would need a template to increase the length of data to be hashed. This turned out to be tricky since underlying hash function is very sensitive to the characters/bytes being used. I also needed to nullify the effect of the template on the original data to be hashed and finally ended up with following code:

def augment_data(data:str) -> str:

    FREQUENCY = "etaonrishdlfcmugypwbvkjxzq"      # frequency table, from most frequent to least frequent.
    sample_dict = {}
    for i, character in enumerate(FREQUENCY):
        sample_dict[character] = FREQUENCY[len(FREQUENCY) -1 -i]

    template_string = "this is {}-{}-{} destined to be a value, otherwise would not have enough variation to begin with in the first place."

    # prevent amplification...
    for d in data:
        template_string = template_string.replace(d,"*")

    new_data = ""
    for d in data:
        if d in sample_dict:
            new_data += sample_dict[d]
        else:
            new_data += d

    return template_string.format(new_data, new_data, new_data )

Idea is to substitute each character in the original data with character we get by reversing the frequency table for english characters. For example e is most frequent letter for english language, we substitute each e for q (which is the least frequent character for english). This way we try to minimize the effect of template string's characters/bytes in the final HASH. We also replace common characters for template string and original data with *, to prevent amplification and bias due to template string chosen. The above routine can be experimented with based on different languages as it uses language specific statistics.

The above strategy results in enough variation for augmented data to fill more than 50 percent of Buckets to get an usable HASH.

We already have compare_hash(data_hash:str, query_hash:str) and generate_hash(data:str), routines available from LSH implementation, So a very simple implementation for Fuzzy Search could look this: 

# possible implementation
# We would create a``hash`` for every data being ``appended/added`` and during query just go over all the indexed ``hashes`` to get top k most similar indices/hashes.

idx_2_data = [] # one to one mapping.
idx_2_hash = [] # one to one mapping.

def generate_hash(data:str) -> str:
    encoded_data = data.encode("utf8")
    ....

def compare_hash(data_hash:str, query_hash:str) -> float:
    ....          # comes from LSH implementation

def append(original_data:str):
    if (original_data not indexed):
        idx_2_data[len(idx_2_data)] = data
        idx_2_hash[len(idx_2_data)] = generate_hash(augment_data(original_data))
    else:
        pass

def suggest(query:str, top_k:12):
    idx_scores = []
    query_hash = generate_hash(augment_data(query))

    for idx, data_hash in idx_2_hash.items():
        score = (compare_hash(query_hash, data_hash))        # this should be fast if to use for a large number of data!!
        idx_scores.append((idx, score))

    sorted_idxScores = sorted(idx_scores, key = lambda x: x[1], reverse = False)[:top_k]

    # extract the original data
    return [idx_2_data[ix] for ix,_ in sorted_idxScores]

Such implementation would work in theory but production may face issues like:

A more practical implementation would also store LSH hash for subwords in original data, like for pulp fiction,we store generated hash for both pulp and fiction assuming space as separator.

# assuming data: ``pulp fiction`` and ``monty python``
# equivalent to an unigram index.

firstcharacter_to_idxHash = {..., 
    "p" -> { (5, hash(pulp), (6, hash(python)) },
    "f" -> { (5, hash(fiction))},
    "m" -> { (6, hash(monty)) }
    ...
}

During query, if a user enters pu, then:

    # possible candidates having first character as ``p``
    query_hash = generate_hash(augment_data("pu"))
    idx_scores = []

    for idx, data_hash in firstcharacter_to_idxHash("p"):
        idx_scores.append((idx, compare_hash(data_hash, query_hash)))

    sorted_idxScores = sorted(idx_scores, ....)[:top_k]   # or a fixed number of candidates. 

    possible candidates = idx_2_data[ix] for ix,_ in sorted_idxScores]

    # re-rank them based on domain specific function.

    # return.

For queries having multiple subwords (splittable by some character like space), we run a for loop collecting a fixed number of candidates for each of subwords. For example, given a query puld ficton we collect 20 unique candidates for puld and 20 unique candidates for ficton, hence ending up with total 40 top candidates. We collect corresponding original data for each of these candidates.

Since collected candidates for each of subword like puld are constrained over that subword only, meaning it may be possible that an actual movie title has puld <something other than fiction> in it, hence would be included in candidates even though being a bad suggestion. We may have to apply some normalization across collected candidates constrained over original query entered by user. This leads to a re-ranking strategy as follows:

suggestions = ["pulp fiction", "monty python", ...]  # possible candidates based on the LSH comparison.
original_query = "puld ficton"                       # original query
split_query = ["puld", "ficton"]                     # we split it based on the space character.

scores_candidates = []
for suggestion in suggestions:
    score = 0

    # if exact match with one of the subwords in query. Boost the score.
    if suggestion in split_query:
        score += 1
        split_query.pop(split_query.index(suggestion))       # to prevent comparing again with same value.
        continue

        # if first character match with on of the subwords in query. Boost the score.
        for d in split_query:
            if d[0] == suggestion[0]:

                if suggestion not in ["a", "an", "the", "and", "in", "of", "this"]: # very common words, user rarely enters that and they are just useless.
                    score += 0.1
                    split_query.pop(split_query.index(d))
    scores_candidates.append((score, suggestion))

# sort the scores_candidates
.. = sorted(scores_candidates, ...)

There is definitely some bias associated with the above discussed strategy, but works great for most of the use-cases, as the term we would be searching is already supposed to be unique enough. That is the logic behind naming things anyway.

Even if we assume that above implementation works surprisingly well, we still need it to be fast to be of any practical usage.

Need for Speed:

Python may not be the best languages to develop algorithms in for real-time applications, as it is relatively slow than most of the AOT compiled languages.

Compare_hash function written in pure python takes around 25 microseconds, Running it alone assuming no extra code in suggest routine for 100k of the stored hashes would result in ~2.5 seconds, so may not be so useful for real time suggestions.

Speeding this function may lead to practical usage of our implementation. I ported the compare_hash to Nim and exposed it as one of functions in the corresponding compiled extension. I also ported the generate_hash as it would not hurt to generate hash much more quickly during append stage. Resulting compare_hash runs at about 5 microsecond on my Intel(R) Core(TM) i5-8300H CPU @ 2.30GHz. CPUs with faster single-thread performance would definitely speed up hash-comparison for both Python and Nim code.

Nim code runs in single threaded mode, without any optimizations like SIMD, which could be explored in the future along with multi-threading!

A good typing rate is 40-50 words per minute, which amounts to around 250ms per character assuming average word length as 4. If we are using it to get suggestions as we type, above implementation should lead to smooth experience definitely for 100k strings, and may be with even 1 Million with some optimizations.

Testing:

What about real world performance ?

I downloaded Wikipedia Movie Plots dataset (hate that kaggle forces login even for user curated datasets!). and indexed/appended 30k movie titles.

Dataset includes movies' titles from all around the world in english language, and hence should make a good enough test-set for evaluation.

A typical search timings looks like this: alt query timings

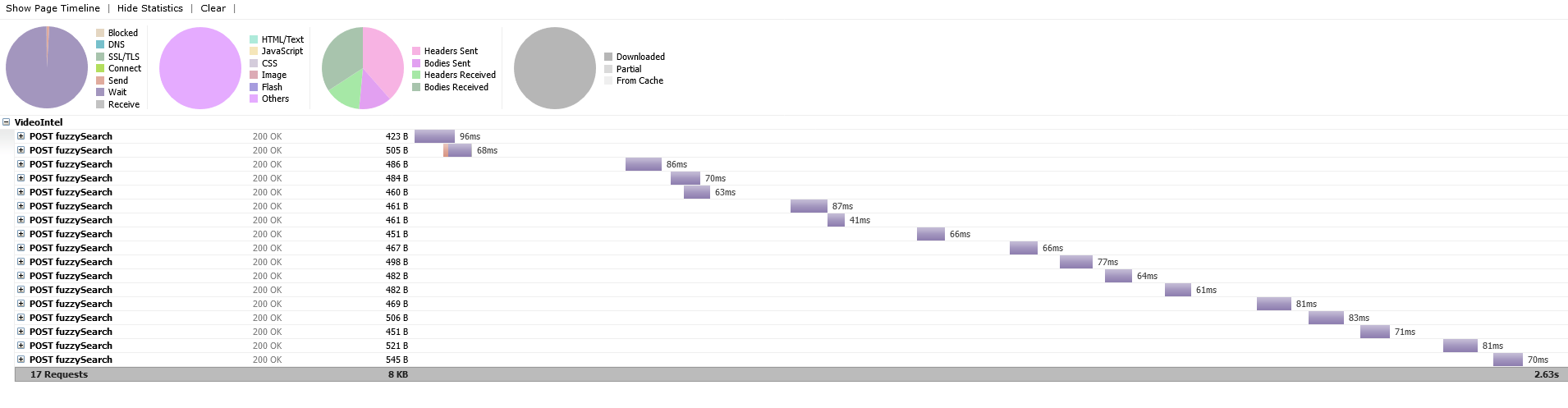
And a short video displaying results in realtime on above said dataset.

I still haven't implemented a simple cache, i.e given a query pulp fiction, pulp subword is being processed again and again, for each character in fiction.

With this implementation average latency seems to be ~25 ms for 30k strings. It may not be that fast, but highly useful to almost all text-interfaces for real time suggestions. Note that some of re-ranking and augmentation logic does assume english as the target language, and user may need to alter such logic to best fit a different language. But there is nothing to suggest that same type of ideas wouldn't work for other domain/language.

Remarks:

Since LSH work directly on bytes, it can be used to hash any resource, be it a pdf, image or any text file. It even can be used to find similar images, or similar paragraphs from a text. Almost no preprocessing is needed to produce an usable hash. You can always improve it with domain specific post-processing. It is also not resource intensive like ML algorithms and follows a standard interface. (convert data into bytes and hash it.) Generated hashes are of fixed size and much easier to store.

It can be a great candidate to augment traditional search along with other approaches like ML.

On the other note, Search still remains a very interesting problem because constraints keep changing depending upon the application, size of the data (useful and/or spam), personal preferences etc. Amount of data a single user stores has also become much larger and there should be more options catering to that. Windows shitty search remains the baseline. I don't have much experience in building search engines, but found it always a good technique to collect a diverse set of possible candidates using various (independent) signals like naive string matching, bag of words, fuzzy, ML. as it can later allow to improve personal search by adjusting the weights of those signals alone. Personal projects can be test-bed to explore some of offbeat/old/weird techniques and fuse them to improve upon baselines.

If you have found this content useful, please consider Donating . It would help me pay my bills and create more of this.